Dammit Jim!

After making the WP_MonsterID WordPress plugin to create a random monster avatar from an assortment of parts for each commenter (based on other people’s code), fruityoaty asked This looks nifty, but how many monster images are available for assigning?

I’d been meaning to calculate this anyway so I did the math and posted it in the comments:

The current part totals are: 17 eyes, 8 hairs, 12 mouths, 15 bodies, 10 legs. That is 244,800 possible combinations. In addition, the body color can range between 20-235 for red, green, and blue. If we count that as 20 distinguishable values for red, green, and blue that adds 8000 possible colors and brings the unique monster count to 2 billion. The only problem is that the algorithm is only using the first 6 digits of the md5 hash of the email which only provides 16 million possible combinations. So I guess the answer is 16 million monsters currently and in the next release I’ll use a few more digits of the hash and increase it to a billion or so. Edit: I did change this so in version 0.3 and later there should be a couple billion possibilities.

Calculating this got me wondering how many unique users it would take before there was likely to be a duplicate monster. For two users it was easy (1 out of 2 billion) but as the number of users increased things got messy since each new monster could match any of the prior monsters. Luckily I remembered enough of my stats class to google for something on calculating the chance of people in a group sharing a birthday.

If you’ve never heard of this problem, stop and take a quick guess for how many people you think it would take for the odds to be better than 50% for two people sharing a birthday. Or as my statistics professor put it, There are twenty-five people in the room will you bet me that no one shares the same birthday?

…

…

Guessed?

Now I know just enough statistics to know betting against a statistics professor is a bad idea but I have to say, at the time, I thought it would have been a fairly good bet. It turns out that I, like most non-statistics professors, underestimated the chance of any two people in a group sharing the same birthday. Actually, if there are 23 people in a room there is a greater than 50% chance that at least two will share a birthday. If there are 47 people in a room, there is a 95% chance that at least one pair share a birthday. This greatly increasing probability occurs because like the monsters each person added to the room can match any of the previous people (the 5th person can match person 1,2,3,4; the 25th person can match person 1,2,3,4,5,6,…,24;…).

All this was interesting in understanding the problem but didn’t really get any closer to finding the probability. Luckily Wikipedia provides an approximation for determining the number of people at a given probability of overlap:

Substituting in 2 billion for 365, results in a probablity of overlap that looks like:

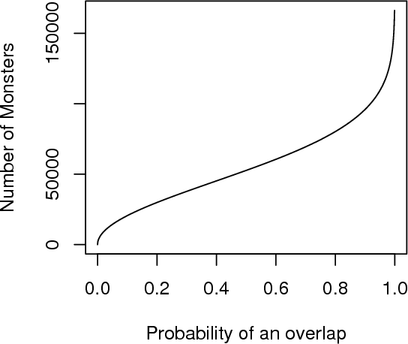
Even with 2 billion monsters there is still a 50% chance of overlap with only 52,000 monsters and a 1 out of 10 chance of overlap with only 20,000 monsters. Most unintuitive to me is that there’s a 99% chance of overlap with only 135,000 monsters. The chances of an overlap really does pile up as the number of already present monsters grow. In the plus side, most normal sized blogs should be safe from monster overlap with only a .1% chance of overlap even with 2000 commenters.

So what does all this mean? Well besides not getting suckered in any birthday betting, it’s a good reminder to be careful about assuming uniqueness among a group just because the chance of a match is rare. For example, if in some application each user was assigned a random key of 4 digits (10000 possible combinations). There would be a greater than 50% chance of overlap after only 1% (117 users) of the keys were assigned.

If any one feels like messing around with the calculations themselves here’s the function in R to calculate the miminimum number of assignments to reach a certain probability of overlap from a total number of possible combinations. I’m sure it would be trivial to convert to any other language. Note that’s natural log not log10. number_assignments=function(total_number,probability_overlap){sqrt(2*total_number*log(1/(1-probability_overlap)))}